Our postdoctoral researcher Fernando J. Gómez-Ruiz together with a team of researchers from Donostia International Physics Center, Universidad de la Laguna, and the University of Luxembourg introduced the spin-vector Langevin model as an alternative benchmark for the performance of a quantum annealer.
State-of-the-art quantum annealers are an example of noisy intermediate-scale quantum devices in which the actual dynamics are not expected to be unitary, as various noise sources can give rise to decoherence. Decoherence is broadly acknowledged as being responsible for the emergence of classical behavior in quantum systems. It hampers the potential of quantum computers to exhibit a quantum advantage over their classical counterpart. Benchmarking the performance of quantum annealers against classical models has thus become a central goal.
In the last few years, a heated debate between claims by companies such as D-Wave on quantum annealing being contested by demonstration of classical algorithms with similar performance. Benchmarking complex quantum simulators is a hard problem. This debate eventually becomes constructive and central to progress. Yet, today a single theoretical model due to Smith and Smolin describing planar rotors evolving with Monte Carlo steps (so-called Spin-Vector Monte Carlo model (SVMC)) is broadly embraced by the adiabatic quantum computing community as the ultimate classicality test [1,2]. If a simulator disagrees with SVMC, many argue quantum signatures are at play, even if there is potentially room for other classical models to account for such behavior. Leading experts in the field have stated that “when you think it through in-depth, the SVMC is the only game in town”.
In a recent study published in Physical Review Research [3], the authors introduced a classical model of planar rotors evolving under Langevin dynamics which they shall be referred to as the Spin-Vector Langevin (SVL) model. Classical Langevin dynamics provides a natural setting to describe evolution in real-time and accommodates the interplay between dissipation and thermal fluctuations. They use SVL to describe the dynamics across the phase transition in the transverse-field Ising model. Recently it was used to probe the dynamics in quantum annealers in D-Wave devices which were found inconsistent with SVMC and described by a quantum spin-boson model in previous work [4]. They have shown that SVL can account for the observed behavior, leaving no room for quantum advantage in such settings/devices. Specifically, They had shown that the SVL annealing dynamics yield a power-law scaling for the average density of topological defects as a function of the annealing time.
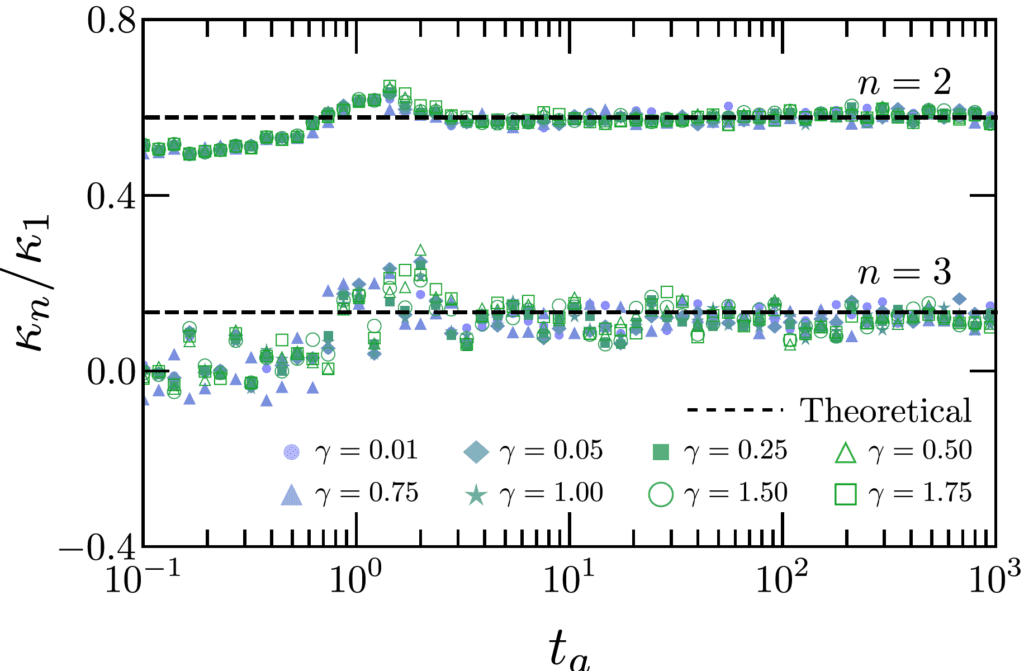
The power-law exponent continuously interpolates between the Kibble-Zurek prediction for the underdamped and overdamped regimes. The SVL model dynamics span the power-law exponents reported in the D-Wave machine and the spin-boson approach, in the classical realm. Additionally, They analyzed the kink number statistics in which all cumulants share the same power-law scaling with the annealing time, as a signature of universality beyond the scope of the Kibble-Zurek mechanism. Cumulant ratios are thus fixed and those reported in D-Wave are further reproduced by SVL.
[1] S. W. Shin, G. Smith, J. A. Smolin, and U. Vazirani, How “quantum” is the D-wave machine? arXiv:1401.7087 (2014).
[2] J. A. Smolin and G. Smith, Classical signature of quantum annealing, Frontiers in Physics 2, 52 (2014).
[3] A. Subires, F. J. Gómez-Ruiz, A. Ruiz-García, D. Alonso, and A. del Campo, Phys. Rev. Research 4, 023104 (2022).
[4] Y. Bando, Y. Susa, H. Oshiyama, N. Shibata, M. Ohzeki, F. J. Gómez-Ruiz, D. A. Lidar, S. Suzuki, A. del Campo, and H. Nishimori, Phys. Rev. Research 2, 033369 (2020).